Reliable Change Index Score

In addition to the presentation of both raw and percentile-based scores, the software also calculates RCI scores that provide information about the magnitude of change from baseline testing performance to post-injury. If a particular score is significantly different from the baseline score obtained by the test taker, the scores are printed in red on the Clinical Report. Some variation and test score change over repeated administrations is to be expected. The issue for healthcare professionals is to determine when this change is significant and clinically meaningful. ImPACT Version 4 provides Reliable Change Index Scores (RCI’s) for each Module, Composite and Two-Factor Score. The reliable change methodology allows the clinician to reduce the adverse impact of measurement error on test interpretation. To represent clinically significant improvement, the change score must be statistically reliable. However, the converse is not true; a statistically reliable change does not necessarily guarantee a clinically meaningful change. It is also important to emphasize that an RCI score is not synonymous with a diagnosis.

Calculating the RCI for ImPACT Version 4 remains the same as the previous versions of ImPACT, even when an individual takes a baseline test using a computer mouse and is retested with a post-injury test using a track pad device. (or vice-versa). There are only two conditions where an RCI cannot be calculated:

a) When a potentially invalid Baseline Test ("Baseline ++") is included on a report;
b) When test results with "mixed norms" (tests prior to version 3.8.0 released on 26-Jan-2019 and tests version 3.8.0 or newer) are included on a report.

The Reliable Change Index (RCI) method for interpreting change on neurocognitive tests is a well-accepted method for determining change. This method relies heavily on the standard error of the difference score. The standard error of the difference (Sdiff) can be used to create a confidence interval (i.e., a prediction interval in the statistical literature) for a test-retest difference score. Essentially, this confidence interval represents the probable range of measurement error for the distribution of difference scores.

RCI scores were calculated to provide an index of change from baseline to post-injury. RCI scores were calculated by an independent professional statistician based on methodology described in detail by Iverson et al. (2003) and Jacobson & Truax, (1991) to assess whether a change among repeated assessments was reliable and meaningful. The RCI provides an estimate of the probability that a given difference between a test taker’s scores would not be obtained as a result of measurement error (Iverson, Sawyer, McCracken, Kozora, 2001). This allows clinicians to reduce any effects of measurement error, usually in the form of practice effects (Iverson, Brooks, Collins, Lovell, 2006), inattentiveness or fatigue.

Given two assessment scores (Time 1 and Time 2), calculation of RCIs involves the use of the standard error of difference (Sdiff), which is used to create a confidence interval around the two baseline assessment scores. The formula for Sdiff is provided below.

Participants#

The first sample was comprised of 56 adolescents and young adults who completed the ImPACT test twice for the purpose of a test-retest study. There were 29 males and 27 females. Their average age was 17.6 years (SD=1.7, range=15–22). Approximately 64% were in high school and 36% were in university. The average retest interval was 5.8 days (median=7, SD=3.0, range=1–13). Approximately 29% were retested within 3 days, 43% within 4 days, 82% within 7 days, and 95% within 11 days.

The second sample was comprised of 41 amateur athletes who sustained a sports-related concussion.

All athletes completed ImPACT at the beginning of the season. All were retested within 72 hours of their concussions (mean=1.3, median=1, SD=0.7 days). This sample was 90% male. Their average age was 16.8 years (median=16, SD=2.4, range=13–22).

Approximately 71% were in high school and 29% were in university. The vast majority of athletes were football players (88%), with small numbers of athletes in other sports such as hockey, soccer, basketball, and wrestling.

Most athletes had sufficient information to classify the severity of their concussions using the American Academy of Neurology Concussion Grading System. Approximately 54% had Grade I Concussions, 22% had Grade II Concussions, and 7% had Grade III Concussions. Missing data prevented the confident classification of 17% (i.e., 7 athletes).

Design#

The first set of analyses were based on the healthy young people tested twice. Relative position across the two distributions was examined with a Pearson correlation. Level of performance within subjects was examined with dependent t-tests. Reliable change estimates were derived from a modification of the method proposed by Jacobson and Truax (1991).

Results#

The descriptive statistics, standard errors of measurement (SEMs), standard errors of difference (Sdiff), and reliable change confidence intervals are presented in the Table below.

The Pearson test-retest correlation coefficients for the composite scores were as follows:

• Verbal Memory = .70,
• Visual Memory = .67,
• Reaction Time = .79,
• Processing Speed = .86,
• Post-concussion Scale = .65.

These coefficients are used in the calculation of the RCI, which are referred to as r12 test-retest coefficients.

The Mean and SD by composite with the calculated Sdiff is presented in the Table 1.

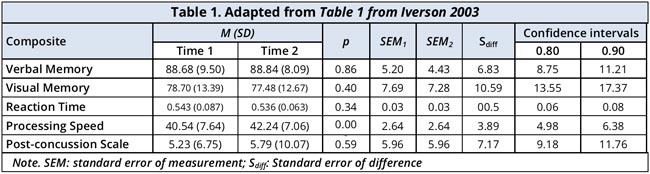
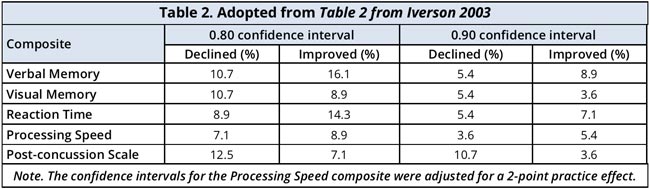
The reliable change difference scores associated with the two confidence intervals were applied to the original data. If the distributions of difference scores were perfectly normal, then one would expect to see 10% in each tail for the 0.80 confidence interval and 5% in each tail for the 0.90 confidence interval. As seen in Table 4, the percentages of subjects that would be classified as reliably improved or declined was reasonably close to what would be predicted from the theoretical normal distribution.

The number of scores that reliably declined for each subject was computed. A decline was defined as reliably lower Verbal or Visual Memory, slower processing speed or reaction time, or greater symptoms at retest versus baseline (80% confidence interval). The percentages of subjects showing declines across the five composite scores are as follows: no declines = 63.0%, one decline = 39.3%, two declines = 1.8%, 3 declines = 0%, and 4 declines = 1.8%.
It should be noted that adjustments of 2 points were made to the ImPACT Processing Speed composite score to account for practice effects. It was not necessary to adjust the other composite scores because practice effects were not identified. ImPACT was designed to reduce practice effects through randomization of stimuli presentation. This was an essential design feature because the battery is intended to be used repeatedly, over short intervals.

The reliable change methodology allows the clinician to reduce the adverse effect of measurement error on test interpretation. Clinically significant improvement can only be identified using this approach if the change score is statistically reliable. However, a statistically reliable change does not guarantee a clinically meaningful change. For that reason, we recommend that change scores found to be significant should be areas the clinician focus attention on for further investigation. We do not suggest that statistically significant changes are synonymous with clinically significant events.